Ei god innføringsbok i R vil mange ha glede av, og ei eksempelbasert bok høyrest ut som ein veldig god idé, med stort potensial. Dessverre utnyttar ikkje denne boka potensialet. Boka skryt av «interesting applications with real data» og eksempel som «reflect good statistical practice». Eg synest ingen av delane stemmer.
Målgruppa er folk som har tatt, eller tar, nokre statistikkurs, og som ønskjer å læra å gjera dei statistiske analysane frå desse i R. Ho krev (visstnok) ingen forkunnskapar i R eller i annan programvare (!).
Kvart kapittel tar for seg eit statistisk emne (for eksempel regresjon), som vert illustrert med ulike analyseeksempel og R-kode for desse, etterfølgt av eit lite sett oppgåver. Datasetta som vert brukte, finst på nettsida til boka eller i ulike R-pakkar.
Sidan eg ikkje er spesielt fornøgd med boka, er denne bokmeldinga meir ei opplisting av enkeltelement eg ikkje likte, og påpeiking av feil og manglar. Forhåpentlegvis vil denne lista vera til nytte og rettleiing for dei som har kjøpt og brukar boka.
Kapittel 1 – Introduction
Første kapittel er eit introduksjonskapittel, med ein heilt grei gjennomgang av nokre grunnleggande R-kommandoar, med nokre enkle og nokre litt småavanserte eksempel. Ein pussig ting er at forklaringa om korleis vektorar, matriser og lister – heilt grunnleggande datastrukturar i R – fungerer, ikkje står her, men i eit appendiks heilt bak i boka. Appendikset er nødvendig for å forstå resten av boka. Råd for nybegynnarar: Les dei tre første sidene i kapittel 1, so appendikset, og so resten av kapittel 1.
Ein ting som går igjen i boka er at forfattarane ikkje ser ut til å ha bestemt seg på kva nivå teksten skal ligga. Nokre plassar er ting forklart som om ein ikkje kan noko som helst, og andre plassar verkar det som om ein antar at lesaren er ekspert både på R og statistikk. I andre avsnitt i introduksjonskapittelet forklarar dei for eksempel slik kva R-språket er:
This language provides the logical control of branching and looping, and modular programming using functions.
Klart forståeleg for ein programmerar, sjølvsagt, men for ein person utan forkunnskapar i R eller annan programvare?
Det er for øvrig svært uheldig at boka baserer seg på at brukaren skal bruka R direkte, med det minimale og lite brukarvenlege standardbrukargrensesnittet, i staden for for eksempel RStudio, som er brukarvenleg både for nybegynnarar og avanserte brukarar.
I introduksjonskapittelet lærer ein heldigvis korleis hjelpesystemet i R fungerer. Men her kunne med fordel den svært nyttige apropos()-kommandoen vore nemnt (skriv apropos("test") for ei oversikt over funksjonar med «test» i namnet), og kanskje ogso sos-pakken (for å finna funksjonar i både installerte og ikkje-installerte pakkar).
Til slutt eit liten kommentar om attach()-funksjonen. Forfattarane nemner i dette kapittelet at han kan vera problematisk, men nyttig. Mitt synspunktet (som R-brukar sidan 2003) er at denne funksjonen aldri bør brukast. Han gjer mykje meir skade enn den tilsynelatande nytten han har.
Oppgåvene: Uklar tekst i oppgåve 1.3. I oppgåve 1.4 skal suksessannsynet vera 1/6, ikkje 1/3, som er oppgjeve.
Kapittel 2 – Quantitative Data
Her lærer me numeriske og grafiske samandrag av taldata. Det er nokre OK eksempel på begge delar, men forfattarane brukar den håplaust gammaldagse funksjonen by() for å laga statistikk per gruppe. Bruk heller dplyr-pakken (gjerne saman med tidyr-pakken) eller plyr-pakken. Då vert alt enklare, raskare og meir fleksibelt. Det er ingen vits å anbefala gamle, «tradisjonelle» R-funksjonar når det no finst mykje betre alternativ.
Oppgåvene: Teksten i siste del av oppgåve 2.15 stemmer ikkje, og R-koden er feil.
Kapittel 3 – Categorical Data
Tilsvarande kapittel 2, men no for kategoriske data. Stort sett greitt, men merk at boka sitt forslag på korleis ein finn relative frekvensar (table(x)/length(x)) ikkje er til å stola på. Bruk heller prop.table(table(x)), eventuelt med useNA="ifany"-argument i table()-funksjonen. (Boka si løysing gjev feil svar om x har NA-verdiar.)
I kapittel 1 nemnar forfattarane at ein kan laga reproduserbare R-analysar ved bruk av Sweave-funksjonen. God idé (men merk at ei meir moderne og betre løysing vil vera å bruka knitr-pakken), men dei har tydelegvis ikkje brukt denne sjølv, då R-koden ikkje alltid fungerer. I kapittel 3 har for eksempel variabelen Binom plutseleg bytt namn til Bin, som gjer at R kjem med ei feilmeldinga.
Oppgåvene: I oppgåve 3.3b gjev R åtvaringa «Chi-squared approximation may be incorrect». Det står inga forklaring i boka. Ei løysing er å bruka simulate.p.value = TRUE (eller rekna eksakt p-verdi sjølv – det er ikkje so vanskeleg).
Elles er fleire av oppgåvene her typiske for resten av oppgåvene i boka; dei er ikkje oppgåver ein vert klok av, og dei er ikkje interessante. For eksempel har ein i dette kapittelet fått tak i eit datasett om tvillingar. Tvillingforsking – spennande, tenker du kanskje. Her kan det vera mange interessante analysar å gjera. Men kva analysar får ein beskjed om å gjera? Oppgåve 3.4: Rekn ut frekvensfordelinga til alderen til eine tvillingen. Oppgåve 3.5: Sjekk om det er ein samanheng mellom alder og lønn til eine tvillingen. (Avsløring: Folk som har jobba lenge, tener meir. Og pensjonistar tener ikkje so mykje.)
Kapittel 4 – Presentation Graphics
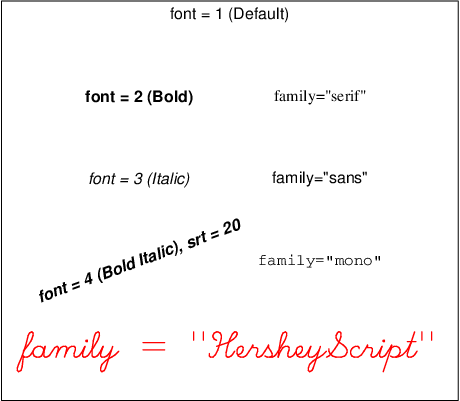God bruk av grafisk dataframstilling er svært nyttig, og bør gjennomsyre ein dataanalyse, og ei bok om R. Grafikk er nemleg verkeleg styrken til R. Ein kan laga ekstremt flotte, avanserte, informative grafiske framstillingar av data. I dette kapittelet lærer ein ikkje noko av dette. Hovuddelen av kapittelet består uinspirerande grafar laga i det gamle base graphics-systemet i R, og esoteriske detaljar rundt dette (eksempelvis korleis laga skråstilt tekst, eller farga tekst i ein handskriftfont).
Heilt til slutt i kapittelet er det bite litt om lattice-pakken, og endå mindre om ggplot2-pakken (berre eitt eksempel!). Dette er dei moderne, kraftige grafikkpakkane for R, der ein svært lett kan laga imponerande, informative plott. Å ikkje skriva eit skikkeleg kapittel om (iallfall éin av) dei er ei stor unnlatingssynd! Oppgåvene er heller ikkje spennande (og éi av dei kan ein ikkje løysa med det ein har lært).
Kapittel 5 – Exploratory Data Analysis
Kjempebra å ha eit kapittel om dette nyttige emnet. Ved hjelp av EDA kan ein oppdaga mange interessante eigenskapar til eit datasett. Men som eksempel brukar forfattarane eit kjedeleg datasett, og gjer banale analysar (oi, det er ein klar samanheng mellom studentfråfall i amerikanske college og prosentdelen som faktisk vert uteksaminert – kven skulle trudd det?!).
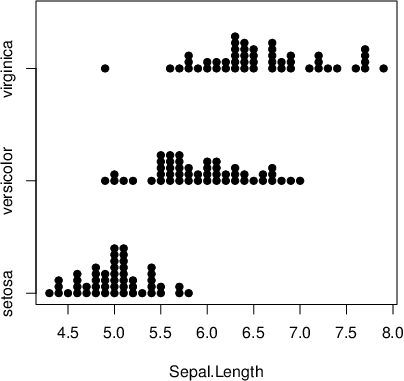Men eg likte at funksjonen stripchart() med argumentet method="stack" var nemnt. Denne kjende eg ikkje til frå før, men han er svært nyttig for å få ei veldig kjapp oversikt over fordelinga til ein (avrunda) kontinuerleg variabel for ulike verdiar av ein kategorisk variabel.
Og boka får pluss for å nemna robuste regresjonslinjer. Men korfor bruka line() i staden for den meir moderne og fleksible rlm(), som òg er lettare å bruka vidare, då ein kan køyra predict(), plot() og liknande direkte på resultatet? Og korfor illustrera robust regresjon på eit datasett der vanleg regresjon fungerer like bra?
Oppgåvene: I oppgåve 5.2 er det avrunda verdiar, so alle punkta vert ikkje synlege på plottet. Bruk heller for eksempel plottefunksjonen sunflowerplot(). Og er det ikkje grenser for kor meiningslause analysar ein skal gjera? Her skal ein «utforska» samanhengen mellom prosent «små klassar» og prosent «store klassar» på amerikanske college (eg har gjort analysen, og kan no avsløra at collega med ein stor del små klassar samtidig er dei collega med ein liten del store klassar!).
Oppgåvene er for øvrig ikkje eingong testa. Prøver ein å køyra kommandoane ein har lært, får ein berre uforståelege feilmeldingar, sidan datasettet inneheld NA-verdiar (som ein ikkje har lært å handtera).
Kapittel 6 – Basic Inference Methods
Tradisjonelt stoff for eit første kurs i statistikk – enkle testar og konfidensintervall. Kanskje litt forvirrande at ein introduserer tre forskjellige testar for prosentverdiar, men pluss for at ein nemner Agresti–Coull-konfidensintervallet. Og ogso litt pussig at ein heile tida ser på 90 %-konfidensintervall (men testar med signifikansnivå på 5 %).
Det er òg rart at ein hevdar Wilcoxon-testen har «less restrictive assumptions» enn ein t-test når ein samtidig føreset at fordelinga skal vera symmetrisk rundt medianen, spesielt når ein vil bruka testen på eit datasett som ein (utan god grunn) var redd for å bruka t-testen på – på grunn av nettopp mangel på symmetri (éin uteliggar). For øvrig bra at kapittelet introduserer ein permutasjonstest, men ein kunne gjerne brukt han på eit datasett der det faktisk var nødvendig, og som var lite nok til ein kunne rekna alle permutasjonane.
Oppgåvene: Oppgåvene består av uinteressante «hypotesar», dels med eit merkeleg forhold til kva som er kjende størrelsar og kva som er ukjende parametrar. Har òg den vanlege misforståinga om at Wilcoxon-testen gjev konfidensintervall for medianar (det er sant om ein antar ei symmetrisk fordeling, men då er medianen lik forventinga, so korfor blanda medianar inn i dette?), eller at Mann–Whitney–Wilcoxon-testen gjev konfidensintervall for differansen av forventingane (eller medianane). Siste oppgåva brukar ein para t-test på observasjonspar som strengt tatt ikkje er uavhengige.
Kapittel 7 – Regression
Ei veldig enkel innføring i regresjon. Brukar eit litt pussig eksempel, der ein prøver å estimera volumet av kirsebærtre som ein lineærsum av høgda og diameteren. Dette hadde vel vore meir naturleg, iallfall som første tilnærming, å sjå på produktet av høgda og kvadratet av diameteren, der ein altso modellerer treet som ein sylinder eller ei kjegle, men dette vert aldri prøvd. Det er òg uheldig/unødvendig bruk av attach()-kommandoen (alle regresjonsfunksjonar tar eit data-argument).
Oppgåvene: I oppgåve 7.5 er estimatet ein får ut heilt på jordet. I oppgåve 7.6 manglar datasettet. Og oppgåve 7.7 er ei fullstendig tullete oppgåve. Her samanliknar ein to verdiar av R², frå same modell med/utan skjeringspunkt. Desse kan ikkje samanliknast, og samanlikninga gjev inga meining! (Sjå artikkelen Model comparisons and R².)
Kapittel 8 – Analysis of Variance I
Eit kapittel med ANOVA-eksempel. Kanskje litt mykje rekneteori (kvadratsummar og sånt), som passar betre i eit statistikkurs? Men eg likte at boka nemner oneway.test(), som er ei utviding av vanleg ANOVA til tilfellet der ein ikkje (nødvendigvis) har like variansar i kvar gruppe.
For øvrig synest eg rein variansanalyse ofte er uinteressant, då det berre gjev p-verdiar og ikkje estimat (og berre eigentleg fungerer for balanserte data). Heldigvis tar boka ogso for seg post hoc-testar for multiple samanlikningar. Men bokas første eksempel er her Fishers LSD-metode! (Som altso ikkje korrigerer for multiple samanlikningar.) Éin metode som kan brukast, er Tukeys HSD-metode, som fornuftig nok ogso vert presentert (merkeleg nok òg med formlar for manuell utrekning).
Oppgåvene: Berre ein liten kommentar til oppgåve 8.1, der ein samanliknar drivstofforbruket til bilar. Med slike data kan ein potensielt få ulike konklusjonar om ein målar drivstofforbruket som liter/mil (slik me gjer i Noreg) eller som mil/liter (som i prinsippet er det ein gjer i USA). Sjå løysinga mi av pusleri nr. 22 i januarnummeret 2008 av Tilfeldig gang for eit rekneeksempel.
Kapittel 9 – Analysis of Variance II
Meir avansert variansanalyse – randomisert blokk-design og tovegs ANOVA. Det er uklart kva forfattarane meiner er forskjellen på desse to designa, men i tovegs ANOVA inkluderer dei ein (potensiell) interaksjon. For randomisert blokk-design brukar dei faktisk R-syntaks for vanleg tovegs ANOVA, y ~ faktor + blokk. Ein meir fornuftig modell for datasettet ville vore y ~ faktor + Error(blokk). No får ein rett nok nøyaktig same svar frå dei to modellane, fordi ein har eit balansert datasett. Men å presentera same modell under to forskjellige namn er meir eigna til å forvirra enn å opplysa.
For øvrig er alle ANOVA-eksempla i boka basert på balanserte datasett. Dette gjer at ein lett kan lura seg sjølv når ein prøver metodane som ein har lært ut på ubalanserte data. R brukar nemleg ein analyse basert på type I-kvadratsummer – sekvensielle testar – og for ubalanserte data er det gjerne ikkje det ein trur ein testar (eller noko som er fornuftig), som ein faktisk testar. (Sjå Venables’ Exegeses on Linear Models.) For øvrig synd at ein aldri nemner at ANOVA og regresjon eigentleg er akkurat det same – lineære modellar.
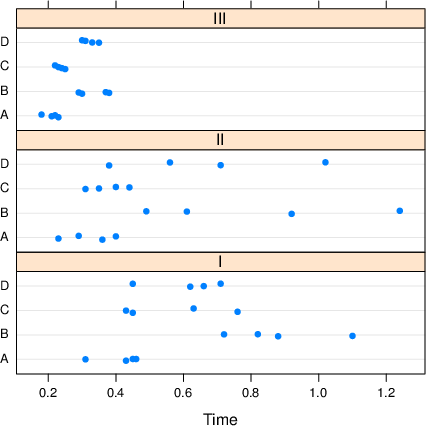I bokas tovegs variansanalyse får ein eit ikkje-signifikant interaksjonsledd (p = 0,11). Dette til tross for at forfattarane presenterer interaksjonsplott som viser rimeleg klart at det er ein interaksjon. Dei ser ikkje ut til å reflektera noko vidare over dette. Men tar ein seg bryet med å faktisk plotta dataa, i staden for å gå rett på modellering og p-verdiar, ser ein straks at ANOVA-modellen deira er heilt på trynet, då dei antar lik varians (homoskedastisitet) på eit datasett som slett ikkje har det (sjå figur). Viss me brukar ein modell som tar omsyn til dette (eksempelvis via gls() i nlme-pakken), er interaksjonen statistisk signifikant med veldig klar margin (p = 0,007).
Oppgåvene: Merk at viss ein les inn datasettet i oppgåve 9.1 slik boka anbefaler, vert siste variabel rekna som numerisk, og resultata frå analysen vert feil. Bruk factor() for å gjera han om til ein faktorvariabel.
Kapittel 10 – Randomization Tests
Bra med eit eige kapittel om dette. Mindre bra at formelen og programkoden for randomiseringstestar er feil. Dei reknar ut p-verdien som talet på «ekstreme» permutasjons-testobservatorar delt på R + 1, der R er talet på permutasjonar. Det er rett at ein bør dela på R + 1, ikkje på R, men då skal den opphavlege testobservatoren ogso inngå i teljaren. Her gjer ein ein dobbeltfeil, og får for låge p-verdiar, som òg kan verta lik 0. Sjå avsnitt 6 i artikkelen Permutation P-values Should Never Be Zero. (For øvrig var det unødvendig å køyra ein randomiseringstest på datasettet i boka, då den vanlege parametriske testen er ganske robust.)
Neste eksempel i kapittelet gjeld talet besøk på ei nettside over tid (målt i vekenummer). Her er endå ein dobbeltfeil. For det første brukar forfattarane eit korrelasjonsmål, viss verdi gjev lite meining, sidan vekenummer ikkje er stokastisk. Dei vil ikkje anta at talet på besøk er normalfordelt, so derfor brukar dei Spearmans korrelasjon. Denne gjev ein p-verdi på 0,06, so forfattarane meiner dei ikkje kan ikkje konkludera at det er nokon trend over tid. Men R klagar, og seier «Cannot compute exact p-values with ties». Randomiseringstestar reddar dagen! Forfattarane lagar ein randomiseringstest som køyrer (vanleg) korrelasjon på rangane av verdiane, og får ut ein (litt feilutrekna, jamfør over) p-verdi på 0,03, «indicating that there is some evidence of a trend of the website hit counts over time». Men vent litt: Er ikkje vanleg korrelasjon rekna ut på rangane det same som Spearmans korrelasjon? Og Spearmans test er jo ein permutasjonstest i seg sjølv. Om Spearmans test ikkje kunne rekna ut nøyaktig p-verdi på grunn av duplikatrangar, korfor gjekk det her?
Forklaringa ligg i at handteringa av duplikatrangar berre er gøymt unna, i ein kommando som sample(rank(x)). Om ein les hjelpesida til rank(), ser ein at duplikatrangar som standard (ties.method="average") får gjennomsnittsverdien rangane ville hatt om dei ikkje var like. So det er berre tilsynelatande at ein løyste problemet. (Og ei teoretisk betre handtering ville vel ha ha vore å brukt ties.method="random".) So eigentleg burde ein fått omtrent same p-verdi som før. Men korfor var p-verdien so mykje mindre? Jo, ser ein nøyare på koden, ser ein at randomiseringstesten reknar ut ein éinsidig p-verdi. Då er det ikkje rart at p-verdien vart halvert! Her har me altso ein feilimplementert og fullstendig unødvendig test som vert tolka feil. Og slik sluttar kapittelet.
Kapittel 11 – Simulation Experiments
Dette kapittelet overraskar, i det at det faktisk er veldig bra. Her lærer ein korleis ein kan estimera sannsyn som er vanskelege å rekna ut analytisk, ved hjelp av simulering. Mange fine eksempel og oppgåver.
Tips: Ein kan lett finna konfidensintervall for sannsynsestimata eller forventingane ved å bruka høvesvis binom.test() eller t.test().
Ein liten kommentar til avsnitt 11.2: Viss Peter startar med null dollar, har han vel strengt tatt ikkje råd til å delta i spelet i det heile tatt … Og på side 258 burde ein unngått å bruka variabelnamnet F, sidan F som standard har verdien FALSE, og dårleg skrivne funksjonar kan anta at verdien alltid er det.
I avsnitt 11.3 er til orientering den asymptotiske verdien til utrekninga på side 265 lik 1/e. Vil du prøva deg på ei litt liknande oppgåve, kan du sjå på pusleri nr. 8 i septembernummeret 2001 av Tilfeldig gang. Og ei liknande oppgåve som den i avsnitt 11.4 finn du i pusleri nr. 34, i marsnummeret 2012. I avsnitt 11.5.1 kan ein løysa oppgåva hakket meir elegant ved å bruka rle()-funksjonen.
Kapittel 12 – Bayesian Modeling
For so vidt kjempebra at dette er med, men her vert det for R-/statistikk-nybegynnaren for komplisert, og for mykje stoff «opp av hatten», utan forklaring. Oppgåvene er òg for enkle i forhold til det kompliserte stoffet (og nesten alle gjeld baseballstatistikk – av avgrensa interesse for oss norskingar).
Kapittel 13 – The Monte Carlo Method of Computing Integrals
I første del av kapittelet lærer me å estimera forventingar og variansar. Stoffet høyrer vel altso eigentleg til i kapittel 11. Ein liten kommentarar: Øvst på side 311 bør «true difference» vera «true expected difference», sidan me lagar konfidensintervall, ikkje prediksjonsintervall.
I resten av kapittelet lærer me å simulera frå vilkårlege fordelingar (stikkord: Metropolis–Hastings og Gibbs-sampling). Teorien er stort sett altfor tung og kort forklart til at ein nybegynnar får mykje ut av det, men kapittelet kan kanskje vera nyttig for dei som har lært om metodane før?
Ein kommentar til side 331: Ved bruk av Gibbs-metoden er observasjonspara ein får ut simulert frå (tilnærma) rett fordeling, men dei er ikkje uavhengige. Dette er viktige å vera klar over dersom ein ønskjer å bruka dei til for eksempel å laga eit konfidensintervall for størrelsen ein parameter. For å få tilnærma uavhengige par, kan ein ta kvart n-te par (for ein passande verdi av n).
I eitt eksempel simulerer ein dekningsgraden til eit konfidensintervall for ei binomisk fordeling – ei nyttig øving. Det er ikkje poenget med kapittelet, men viss ein er interessert i dekningsgraden til slike konfidensintervall, kan ein ogso bruka binom-pakken. For eksempel vil binom::binom.coverage(p=.15, n=20) reprodusera estimatet på side 320.
Oppgåvene: I oppgåve 13.3b er det rart at c = 6 ikkje er eit av alternativa, då dette (beviseleg) er den optimale verdien. (Når ein har normalfordelte data og vil estimera variansen, kan ein altso godt argumentera for at ein bør dela kvadratsummen av avvik frå snittet ikkje på n − 1 men på n + 1.).
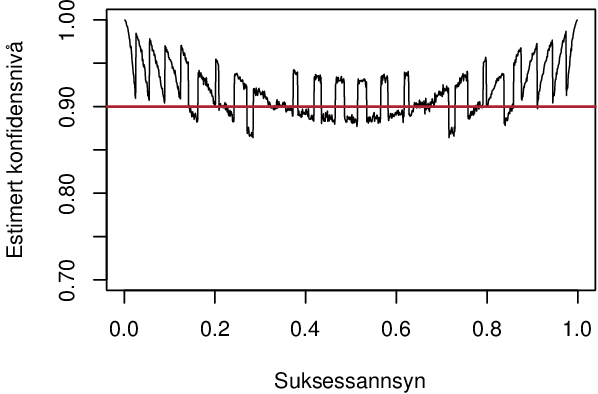
I oppgåve 13.4 er formelen og oppgåva feil. Agresti og Coull sin regel om å legga til to suksessar og to fiaskoar er for 95 %-konfidensintervall, ikkje 90 %-konfidensintervall, som boka ber om. Gjer ein oppgåva slik ho står, ser det ut som metoden fungerer veldig dårleg, spesielt for veldig låge eller høgre suksessannsyn:
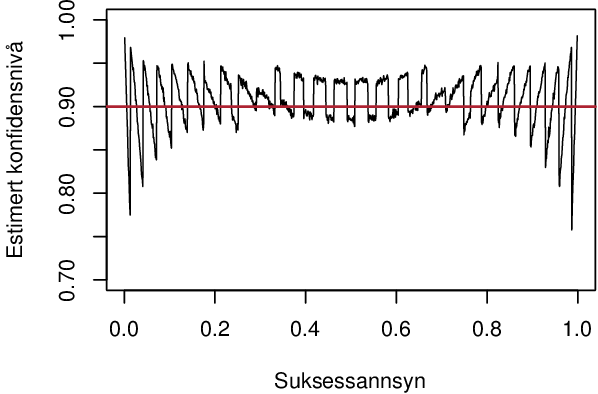
Men for 90 %-konfidensintervall skal ein legga til qnorm(.1/2)^2/2 (altso 1,35) suksessar og fiaskoar, og då går det ganske bra, ogso for svært høge og låge suksessannsyn:
Oppgåve 13.6: Dette er ikkje ein tettleiksfunksjon, slik boka hevdar (kva er det?). I deloppgåve d bør ein bruka ein innbrenningsperiode (kor lang avheng av startverdien ein brukar). Og viss ein lurer, er formlane for faktisk forventing og varians lik a/b og a(1 + b)/b².
Oppsummert
Som ein kan lesa ut frå teksten over, er eg ikkje vidare begeistra for boka. Men når det er sagt, er det heller ikkje ei forferdeleg bok; ein kan læra mykje R av ho (og til og med litt statistikk).
Det eg mislikar mest at ho er ein forspilt sjanse. Ein kunne laga ei bok med gode, interessante eksempel, som illustrerte klok statistisk analyse – som gav innsikt. Det har ein ikkje gjort. Og ein kunne presentert moderne metodar for datahandtering, med bruk av populære tilleggspakkar. Dei gamle standardfunksjonane i R er brukbare, men no finst det nyare metodar som er raskare, meir fleksible og enklare å bruka (pakkane dplyr og tidyr, eller plyr og reshape2). Det same gjeld funksjonar for grafikk/plott (pakkane lattice og ggplot2).
Men alt i alt vil ein som nybegynnar få ei brukbar innføring i delar av R med denne boka. Om ein alt har kjøpt boka, bør ein klart ta seg tid til å arbeida seg gjennom ho. Eg håpar denne utvida bokmeldinga kan vera til hjelp her. Eg har for øvrig gjort nesten alle øvingsoppgåvene, so viss det er nokon som ønskjer kommenterte, utvida løysingsforslag til enkeltkapittel, er det berre å ta kontakt med meg.